Finding the Distance of Nearest Zero in the Matrix
Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.
The distance between two adjacent cells is 1.
Example 1:
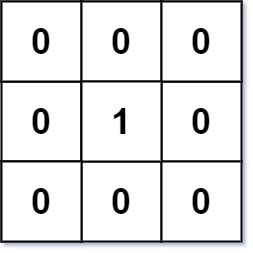
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]
Example 2:
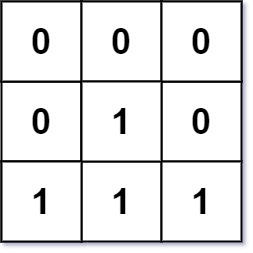
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j]is either0or1.There is at least one
0inmat.
Here is My Solution using BFS:
class Solution {
public int[][] updateMatrix(int[][] mat) {
int m = mat.length;
int n = mat[0].length;
int[][] ans = new int[m][n];
Queue<int[]> q = new LinkedList<>();
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(mat[i][j] == 0){
q.add(new int[]{i,j});
} else {
ans[i][j] = -1;
}
}
}
int dist = 0;
while(!q.isEmpty()){
++ dist;
int size = q.size();
for(int i=0;i<size;i++){
int roco[] = q.peek();
int row = roco[0];
int col = roco[1];
q.remove();
int[][] trav = {{0,-1},{0,1},{-1,0},{1,0}};
for(int[] cur:trav){
int r = row + cur[0];
int c = col + cur[1];
if(r >= 0 && r < m && c >= 0 && c < n && ans[r][c] == -1) {
ans[r][c] = dist;
q.add(new int[]{r,c});
}
}
}
}
return ans;
}
}